Normalising a vector

Contents

Normalising a vector#

Normalising a vector is the process of making the length of a vector equal to 1, while maintaining the direction. This is called a unit vector.

Formula#

\[\overrightarrow{u} = { \overrightarrow{v} \over {\vert\vert\overrightarrow{v} \vert\vert} }\]

Intuition#

Building an understanding of this process. Starting out with a 2D vector \(\lt2, 4\gt\).

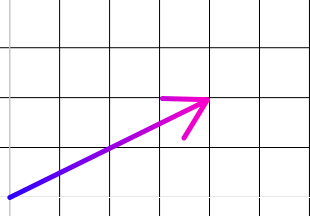
../_images/normalisevectors1.png

We can compute the hypotenuse with Pythagoras.

\(\sqrt{2^2 + 4^2} = \sqrt{20}\)

So the question then becomes, “What can I do to \(\sqrt{20}\) to make it equal to 1”. That’s an easy question to answer, just divide it by itself. BUT the catch is preserving the angle.

Working out the angle we get \(\arcsin({4 \over \sqrt{20}}) \approx 63.43\)

Our unit vector will always be a length of 1. That means our vector point will lie at 63.43 degrees on a unit circle.

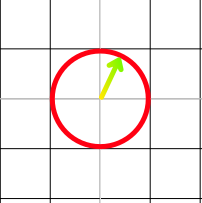
../_images/normalisevectors2.png

To get our values we just plug in 63.43 into cosine and sine.

\[ \begin{align}\begin{aligned}\sin{(63.43)} = 0.89\\\cos{(63.43)} = 0.45\end{aligned}\end{align} \]

Which is just our values of \({4 \over \sqrt{20}}\) and \({2 \over \sqrt{20}}\).

Putting it all together we can say

\[{{\lt2,4\gt} \over \sqrt{20}} = \lt0.45, 0.89\gt\]
Contents